80 最长不下降序列(完结)
最长不下降序列(完结)(一)
-
不下降序列问题 设由n个数组成的数列,记为:a[1]、a[2]、...、a[n],若存在
i1<i2<...<im满足:a[i1]<=a[i2]<=...<=a[im],则称为长度为m的不下降序列。 例如:3,18,7,14,10,12,23,41,16,24 则:- 3,18,23,24,是一个长度为4的不下降序列
- 3,7,10,12,16,24是一个长度为6的不下降序列
问题:如何求最长不下降序列?如何求所有最长不下降序列?
-
问题规模
-
使用数列中的元素和元素间的关系建立图模型
-
图中顶点的附加数据值为对应的数列元素值
-
图中的边按照如下方式建立
当数列中的某个元素与后序元素存在不下降关系时
- 从该元素对应的顶点到后续元素对应的顶点存在一条有向边
- 边的权值固定为1
-
-
-
建模示例:1,3,4,2,5
1 3 4 2 5 0 1 2 3 4 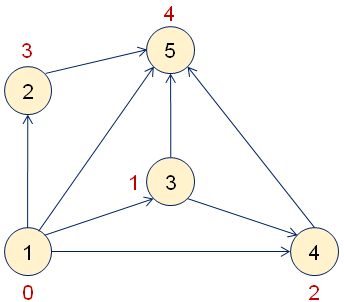
求图中的最多顶点路径(路径上经过的顶点数目最多)。
-
解决思路
- 以每一个顶点作为起始顶点寻找局部最多顶点路径
- v0->p0,v1->p1,...,vn-1->pn-1
- 寻找全局最多顶点的路径
pm=max{p0,p1,...,pn-1}
- 以每一个顶点作为起始顶点寻找局部最多顶点路径
-
局部最多顶点路径的求解思路

- 获取当前顶点v的邻接顶点
{aj0,aj1,...} - 以各个邻接顶点为起点求解最多顶点路径
{paj0,paj1,...} pv=max{paj0,paj1,...}+1
- 获取当前顶点v的邻接顶点
-
原材料
Array<int> count;count[i]表示以i为起始的最多顶点路径上的顶点树
Array<int> path;- path[i]表示以i起始的最多顶点路径上经过第一个顶点
Array<bool> mark;- 如果i起始的最多顶点路径已经找到,则:mark[i]为true
-
寻找局部顶点数最多的路径
- 定义功能:search_max_path(v,count,path,mark)
- 以v作为起始顶点寻找最多顶点路径
- count记录经过的最多顶点树
- path记录最多顶点路径上经过的第一个顶点
- mark记录最多顶点路径是否已经找到
- 定义功能:search_max_path(v,count,path,mark)
编程实验
-
局部最多顶点路径
最长不下降序列(完结)(一)
-
最长不下降序列求解流程
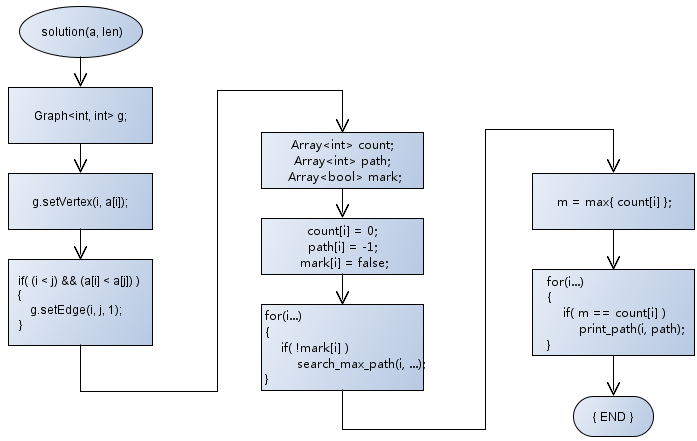
-
最长不下降序列求解流程
void solution(int *a,int len){
DynamicArray<int> count(len);
DynamicArray<int>path(len);
DynamicArray<bool>mark(len);
SharedPointer<Graph<int,int>> g;
g = create_graph(a,len);
init_array(count,path,mark);
search_max_path(g,count,path,mark);
print_max_path(g,path);
}
编程实验
-
最大不下降序列
课程总结
- 数据结构的学习重点在于以下几个方面
- 编程能力的训练(语言强化训练,逻辑思维训练)
- 数据组织方式的训练
- 简单算法设计的训练
- 经典算法的学习
- ......
- 外传篇
- 二分查找
- 字典类型的创建
- 二叉树排序
- 平衡二叉树
- 哈希类型的创建
- ... ...